25 ++ p(x)=3x solution 372150-P(x)=3x solution

Solution set = {15 ≤ x < 5} The solution set can be graphed on the number line as Question 12 Solve and graph the solution set of (i) 2x – 9 < 7 and 3x 9 ≤ 25, x ∈ R (ii) 2x – 9 ≤ 7 and 3x 9 > 25, x ∈ I (iii) x 5 ≥ 4(x – 1) and 3 – 2x < 7, x ∈ R Solution Question 13 Solve and graph the solution set of (i) 3x(iv) p(x)=kx 2 –3xk Solution If x1 is a factor of p(x), then p(1) = 0 By Factor Theorem ⇒ k(1) 2 –3(1)k = 0 ⇒ k−3k = 0 ⇒ 2k−3 = 0 ⇒ k= 3/2 4 Factorize (i) 12x 2 –7x1 Solution Using the splitting the middle term method, We have to find a number whose sum = 7 and product =1×12 = 12If p(x) is a third degree polynomial and q(x) is a fourth degree polynomial then find the degree of p(x) × q(x) Answer i p(x) = x 2 3x 1 , q(x) = 2x – 4

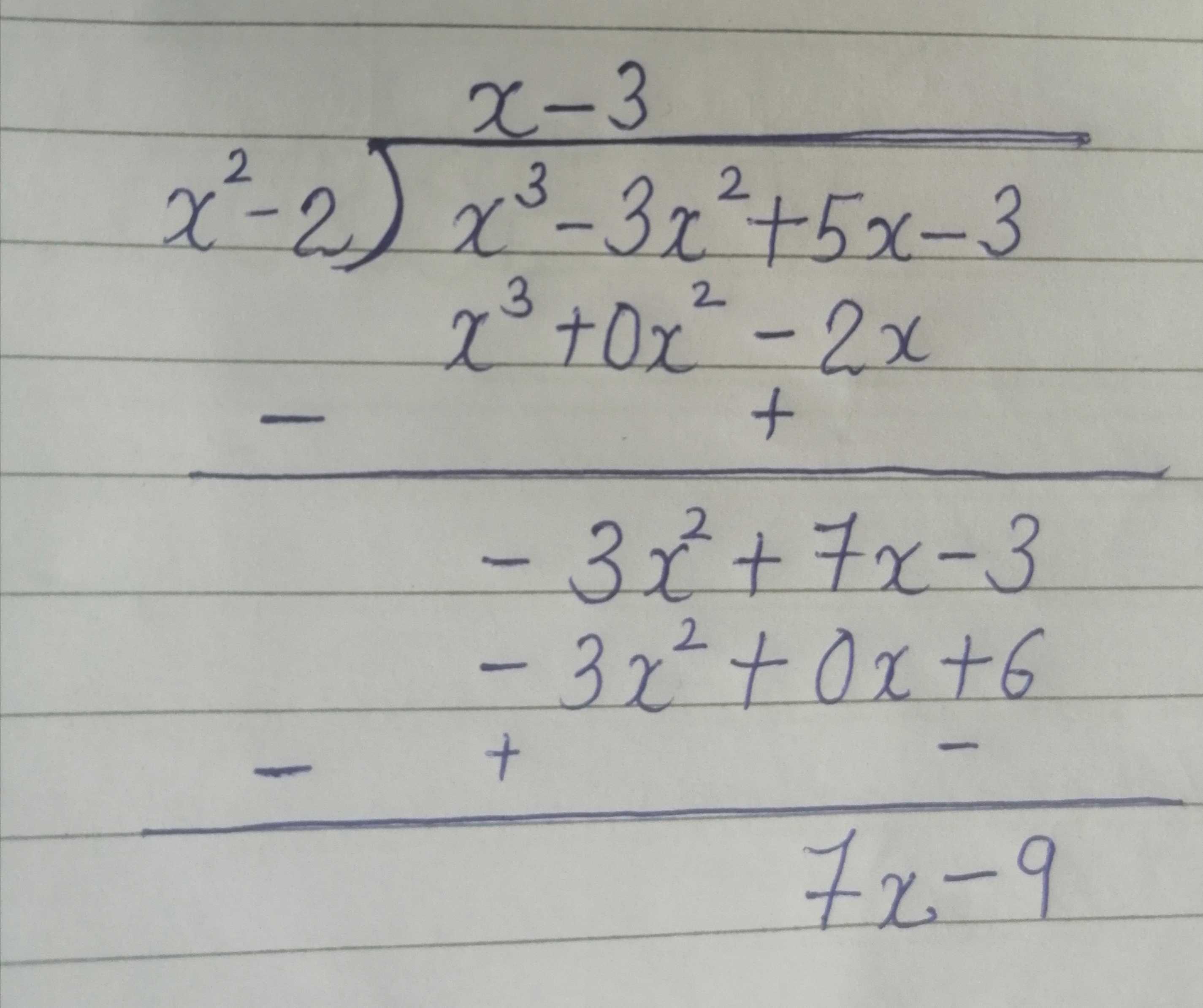
If P X X3 3x2 5x 3 And G X X2 2 Find Remainder Mathematics Topperlearning Com T7tfrb44

P(x)=3x solution

P(x)=3x solution-If P is the solution set of – 3x 4 < 2x – 3, x ∈ N and Q is the solution set of 4x – 5 < 12, x ∈ W, find (i) P ∩ Q (ii) Q – P Answer 33 (i) – 3 x 4 < 2 x – 3 – 3x – 2x < – 3 – 4 => – 5x < – 7 Question 34 A = {x 11x – 5 > 7x 3, x ∈R} and B = {x 18x – 9 ≥ 15 12x, x ∈R}Is x = 5 a solution of the quadratic equation x 2 – 2x – 15 = 0?

5 Solving Polynomial Equations Ppt Download

Remember that if f(x) = Ax^n, then f ' (x) = nAx^(n1) With this in mind, we have P(x) = 3x^2 5x^3 7x^4 3x^5 So P ' (x) = 6x 15x^2 28x^3 15x^4Simplifying p (x) = 3x 14 Multiply p * x px = 3x 14 Reorder the terms px = 14 3x Solving px = 14 3x Solving for variable 'p' Move all terms containing p to the left, all other terms to the right Divide each side by 'x' p = 14x 1 3 Simplifying p = 14x 1 3 Reorder the terms p = 3 14x 1Swap sides so that all variable terms are on the left hand side 3x1=y 3x − 1 = y Add 1 to both sides Add 1 to both sides 3x=y1 3x = y 1 Divide both sides by 3 Divide both sides by 3

Ie say the root is x,then x>=0 As per the question,one of the three roots is 2/3 if all three roots are real,then (2/3) cannot be one of the roots Please check your question and post againPrabhat Edit The three roots (whether real or not) can be found by equating p(x) to zero and then solving the trinomialYou can solve as many equations as you like completely free If you need detailed stepbystep answers you'll have to sign up for Mathway's premium service (provided by a third party)Here, we are given three terms, First term (a 1) = 2xSecond term (a 2) = x 10 Third term (a 3) = 3x 2We need to find the value of x for which these terms are in APSo, in an AP the difference of two adjacent terms is always constant

Find all real zeros of P(x) If neither of these were the instructions, post again and this time give the instructions as to what you are supposed to do with P(x) P(x) = x 5 3x 3 2x 6 x 5 and 3x 3 are both positive, so there is no sign change going from x 5 to 3x 3 3x 3 and 2x are both positive, so there is no sign change going from 3x 3 to 2x 2x is positive and 6 is negative, so that is 1 sign change going from 2x to 6 So there is exactly 1 positive zero of P(x)Solution 2(1) t> Solution 2(2) Solution 2(3) Solution 3 If we divide the total number of chocolates that the student had (x 4 – 3x 3 5x 2 8x 5) by the number of chocolates received by each friend (x 2 – 1), the quotient will give the number of friends and the remainder will give the number of chocolates left over for his teacher Thus, the number of friends = x 2 – 3x 6If p(x)= x 2 – 2√2x1, then find the value of p(2√2) Solution Put x = 2√2 in p(x), we obtain p(2√2) = (2√2) 2 – 2√2(2√2) 1 = (2√2) 2 – (2√2) 2 1 = 1 Question 4 Find the value of m, if x 4 is a factor of the polynomial x 2 3x m Solution Let p(x) = x 2 3x m Since (x 4) or (x – (4)} is a factor of p

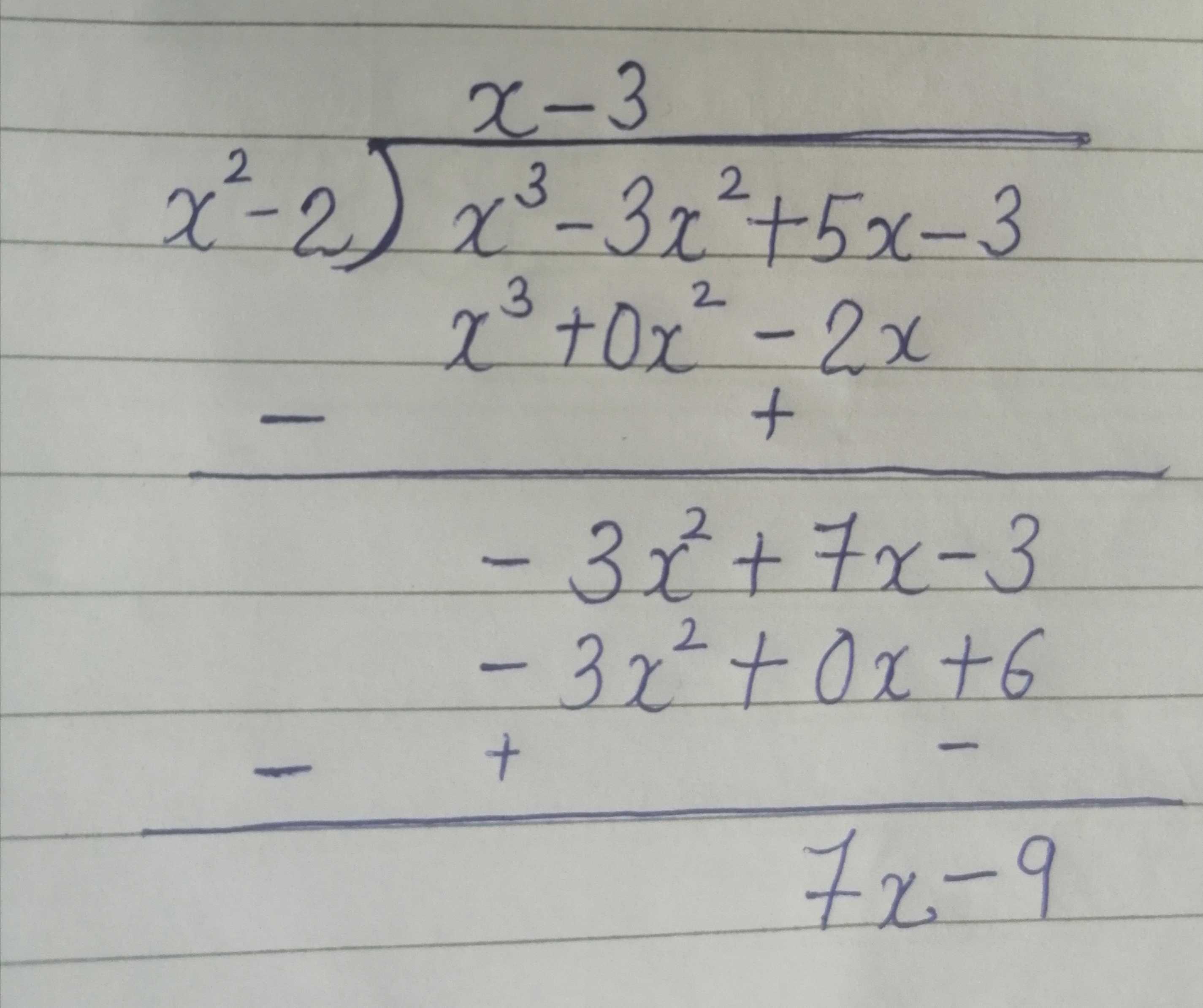
If P X X3 3x2 5x 3 And G X X2 2 Find Remainder Mathematics Topperlearning Com T7tfrb44

Www3 Nd Edu Apilking Math Work Old exams Exam1f08soluutions Pdf

All the solutions of Polynomials Mathematics explained in detail by experts to help students prepare for their CBSE exams R S Aggarwal and V Aggarwal Solutions for Class 9 Mathematics CBSE, 2 Polynomials When p(x) = x 3 3x 2 4x 32 is divided by (x 2), the remainder is (a) 0 (b) 32 (c) 36 (d) 4 Solution 18StepbyStep Solutions Use stepbystep calculators for chemistry, calculus, algebra, trigonometry, equation solving, basic math and more Gain more understanding of your homework with steps and hints guiding you from problems to answers!X^45x^24=0 \sqrt{x1}x=7 \left3x1\right=4 \log _2(x1)=\log _3(27) 3^x=9^{x5} equationcalculator 3x5=14 en Related Symbolab blog posts High School Math Solutions – Quadratic Equations Calculator, Part 1 A quadratic equation is a second degree polynomial having the general form ax^2 bx c = 0, where a

Find Value Of P X 5 X 2 3 X 7 At X 1

Solved 1 21 3x 4x Rear And Z2 3x 2x3 Xe27 Ar Chegg Com

If p(x) is a third degree polynomial and q(x) is a fourth degree polynomial then find the degree of p(x) × q(x) Answer i p(x) = x 2 3x 1 , q(x) = 2x – 4Here, P=y 2 ,Q=xy , R= x(z2y) Hence the general solution is f(x 2 y 2, yzy 2)=0 3Solve(3z4y)p(4x2z)q=2y3x Soln Given (3z4y)p(4x2z)q=2y3x This equation of the form Ppq=R Here, P= (3z4y) ,Q=(4x2z) , R= 2y3x Again use Lagrangian multipliers 2,3,4, 2x3y4z=b Hence the general solution is, F(x 2 y 2 z 2 , 2x3y4z)=0Solution Let p (x) = 3x 3 11x 2 34x 106 p (x) in standard form Coefficients are 3 11 34 106 q(x) = x – 3, its zero x = 3 Synthetic division Quotient is 3x 2 x 94, it is compared with the given quotient 3x 2 ax b Coefficient of x is a = Constant term is b = 94 Remainder r = 3

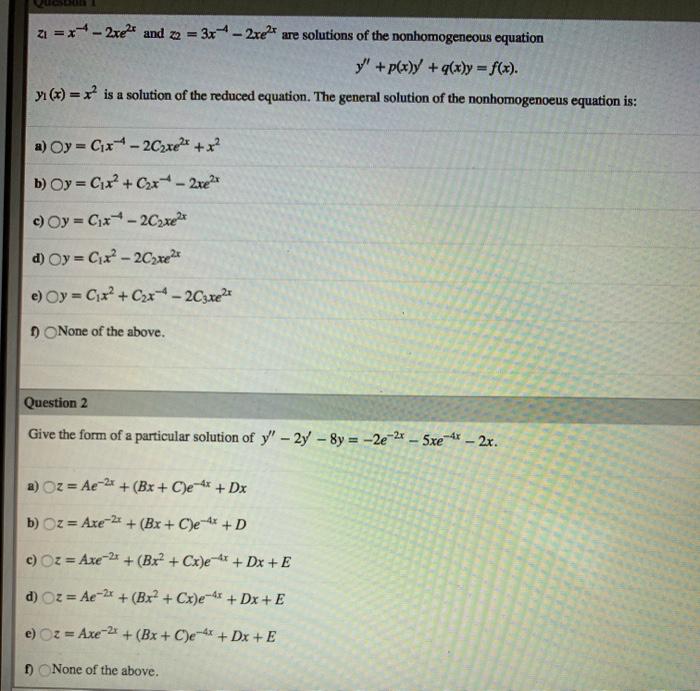
Solved Z1 X 2xet And X2 3x 2xet Are Solutions Of Chegg Com

1 Find The Maximum Revenue If The Price Of Selling X Shoes Is P X 2 Homeworklib

The remainder is zero when f(x) is divided by (x – a) f(a) = 0 The solution to f(x) = 0 is a The zero of the function f(x) is a Example Determine whether x 1 is a factor of the following polynomials a) 3x 4 x 3 – x 2 3x 2 b) x 6 2x(x – 1) – 4 Solution a) Let f(x) = 3x 4 x 3 – x 2 3x 2 f(–1) = 3(–1)4 (–1Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historySolution x 2 – 2x – 15 = 0 For x = 5 to be solution of the given quadratic equation it should satisfy the equation So, substituting x = 5 in the given equation, we get LHS = (5) 2 – 2(5) – 15 = 25 – 10 – 15 = 0 = RHS

Chapter 1 Maths 3

Ex 2 2 4 Find The Zero Of The Polynomial In Each Of Ex 2 2

3 Find the indicated derivative for each function Show your work (Sec 26) Find y000, y= 4x4 x2 7 Solution y0= 16x3 2x y00= 48x2 2 y000= 96x Find d2f dx2, where f(x) = xsinx Solution f0(x) = xcosx sinx f00(x) = cosx xsinx cosx= 2cosx xsinx Find r(4), where r(x) = 1=x Solution r0(x) = 1=x2 r00(x) = 2=x3 r000(x) = 6=x4 r(4)(x) = 24=x5 4 Find a tangent line through the curve 2x 2Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorSolve any equation with this free calculator!

Chapter 1 Maths 3

Polynomials Exercise 2 3 Class 10 Breath Math

Step by step solution Step 1 Equation at the end of step 1 3x • (x 2) = 0 Step 2 Theory Roots of a product 21 A product of several terms equals zero When a product of two or more terms equals zero, then at least one of the terms must be zero We shall now solve each term = 0 separatelyFind g(x) Solution Divided, p(x) = x 3 – 3x 2 x 2 Quotient = (x – 2) Remainder = (2x 4) Let g(x) be the divisor According to the division algorithm, Dividend = Divisor x Quotient Remainder Concept Insight When a polynomial is divided by any other nonzero polynomial, then it satisfies the division algorithm which is as belowIs x = 5 a solution of the quadratic equation x 2 – 2x – 15 = 0?

Tenth Maths Guide For Polynomials Exercise 3 1 3 2 3 3 3 4 Solutions For Class 10 Maths Chapter 3 Maths Glow

Ex 2 2 3 Verify Whether Following Are Zeroes Of The Ex 2 2

A) no solution B) one solution C) two solutions D) infinitely many solutions 9) Which graph represents the solution for the equation 1 2 x 1 = x 2?If P is the solution set of – 3x 4 < 2x – 3, x ∈ N and Q is the solution set of 4x – 5 < 12, x ∈ W, find (i) P ∩ Q (ii) Q – P Solution (i) – 3 x 4 < 2 x – 3 – 3x – 2x < – 3 – 4 => – 5x < – 7 Question 34 A = {x 11x – 5 > 7x 3, x ∈R} and B = {x 18x – 9 ≥ 15 12x, x ∈R}Solution (D) Let p(x) = ax 2 bx c be the required polynomial whose zeroes are 2 and 5 From (i) and (ii), a = 1,b = 3 and c = 10 ∴p(x) = x 2 – 3x – 10 But we know that, if we multiply/divide any polynomial by any arbitrary constant, then the zeroes of polynomial never change ∴ p(x) = kx 2 – 3kx – 10k, where, k is a real number

Module 1 Polynomial Functions

P X 2x Cube 7x Square 9x 13 G X X 3please Solve This Solution Immediately Brainly In

Here we will look at solving a special class of Differential Equations called First Order Linear Differential Equations First Order They are "First Order" when there is only dy dx, not d 2 y dx 2 or d 3 y dx 3 etc Linear A first order differential equation is linear when it can be made to look like this dy dx P(x)y = Q(x) Where P(x) and Q(x) are functions of x To solve it there is aIf α, β Are the Zeros of the Polynomial P(X) = 4x2 3x 7, Then 1 α 1 β is Equal to CBSE CBSE Class 10 Question Papers 6 Textbook Solutions Important Solutions 3114 CBSE Previous Year Question Paper With Solution for Class 12 Commerce;Hence, p(0)= 1, p(1) = 0, p(2) = 3, for the equation p(x) = (x−1)(x1) Question 3 Verify whether the following are zeroes of the polynomial, indicated against them (i) p(x) = 3x1, x=−1/3

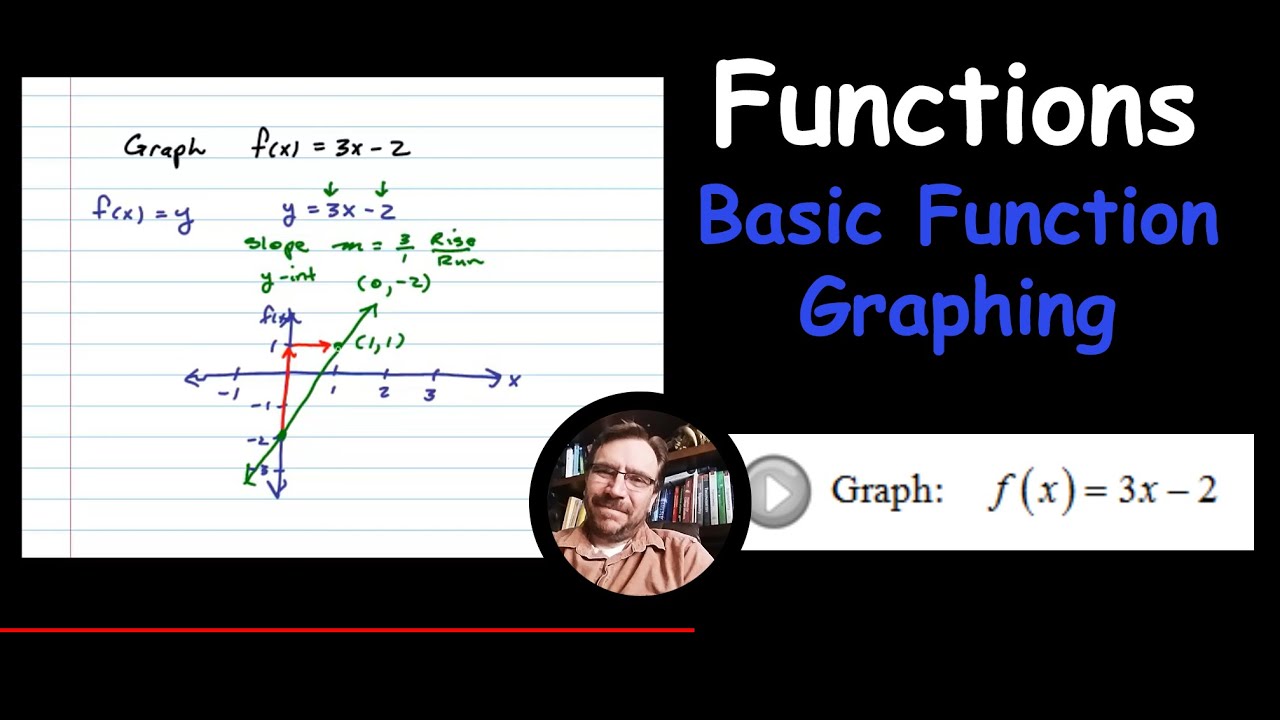
Graph A Linear Function F X 3x 2 Youtube

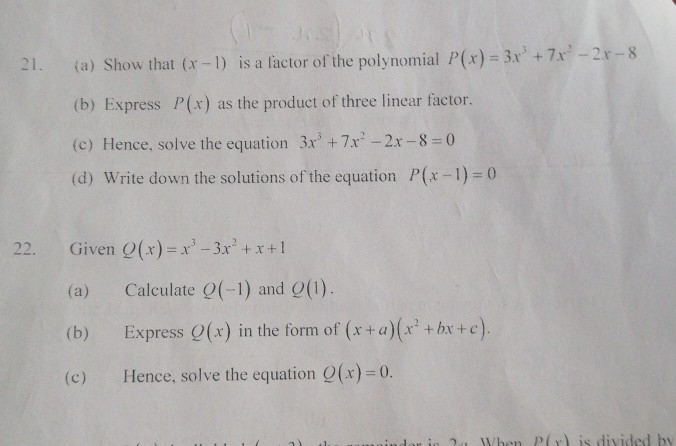
Solved 21 A Show That X 1 Is A Factor Of The Polynom Chegg Com

A) A B) B C) C D) D * Hover over answer image to enlarge 10) x 3y = 5x 6y = 4Remember that if f(x) = Ax^n, then f ' (x) = nAx^(n1) With this in mind, we have P(x) = 3x^2 5x^3 7x^4 3x^5 So P ' (x) = 6x 15x^2 28x^3 15x^4The remainder is zero when f(x) is divided by (x – a) f(a) = 0 The solution to f(x) = 0 is a The zero of the function f(x) is a Example Determine whether x 1 is a factor of the following polynomials a) 3x 4 x 3 – x 2 3x 2 b) x 6 2x(x – 1) – 4 Solution a) Let f(x) = 3x 4 x 3 – x 2 3x 2 f(–1) = 3(–1)4 (–1

If P X 7 3x 2xsquare Then Find The Value Of P 2 P 2 Brainly In

Check Whether 7 3x Is A Factor Of 3x 3 7x With Video Teachoo

Solution The degree of zero polynomial is not defined Question 8 Find the value of the polynomial P(x) = 3x 4 5x 3 5x 2 7x 3 at x = 1 33 55 Correct Option is 2 Solution Given, polynomial is P(x) = 3x 4 5x 3 5x 2 7x 3 Now, at x = 1 P(1) = 3*1 4 5*1 3 5*1 2 7*1 3 = 3 5 5 7 3 = 10 13 = 3Example Divide 3x 3 – 8x 5 by x – 1 Solution The Dividend is 3x 3 – 8x 5 and the divisor is x – 1 After this, the leading term of the dividend is divided by the leading term of the divisor ie 3x 3 ÷ x =3x 2 This result is multiplied by the divisor ie 3x 2 (x 1) = 3x 33x 2 and it is subtracted from the divisor Now again, this result is treated as a dividend and theHow many solutions can be found for the system of linear equations represented on the graph?

Search Q Check Whether 7 2b3x Is A Factor Of 3x3 2b7x Tbm Isch

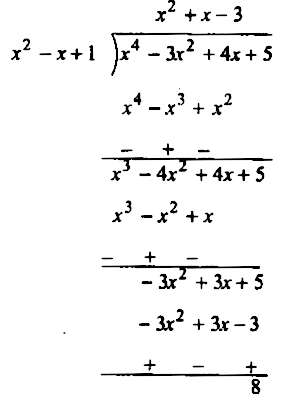
Question Apply The Division Algorithm To Find The Quotient And Remainder On Dividing P X By G X When P X X 4 3x 2 4x 5 G X X 2 1 X Snapsolve

Solution for P(X)=3X^2X4 equation Simplifying P(X) = 3X 2 X 4 Multiply P * X PX = 3X 2 X 4 Reorder the terms PX = 4 X 3X 2 Solving PX = 4 X 3X 2 Solving for variable 'P' Move all terms containing P to the left, all other terms to the right Divide each side by 'X' P = 4X1 1 3X Simplifying P = 4X1 1 3X Reorder the terms P = 1 4X1 3XHere we will look at solving a special class of Differential Equations called First Order Linear Differential Equations First Order They are "First Order" when there is only dy dx, not d 2 y dx 2 or d 3 y dx 3 etc Linear A first order differential equation is linear when it can be made to look like this dy dx P(x)y = Q(x) Where P(x) and Q(x) are functions of x To solve it there is aAfter you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer is right More Examples Here are more examples of how to check your answers with Algebra Calculator Feel free to try them now For x6=2x3, check (correct) solution x=3 x6=2x

Q Tbn And9gcq6gf25op9dejp5qxofv69ixpoa0t3nh9dd6spopldy2pvo9a Usqp Cau

How To Solve 3x Xy 2 Dx X 3 2y Dy 0 Quora

(ii) Find 'a' if the two polynomials ax 3 3x 2 – 9 and 2x 3 4x a, leaves the same remainder when divided by x 3 Solution Question 9 By factor theorem, show that (x 3) and (2x – 1) are factors of 2x 2 5x – 3 Solution Question 10 Show that (x – 2) is a factor of 3x 2 – x – 10 Hence factorise 3x 2 – x – 10Ie say the root is x,then x>=0 As per the question,one of the three roots is 2/3 if all three roots are real,then (2/3) cannot be one of the roots Please check your question and post againPrabhat Edit The three roots (whether real or not) can be found by equating p(x) to zero and then solving the trinomialMathematics 6 Solutions for HWK 22b Section 84 p399 Problem 1, §84 p399 Let T P 2 −→ P 3 be the linear transformation defined by T(p(x)) = xp(x) (a) Find the matrix for T with respect to the standard bases

Verify That 1 And 2 Are The Zeros Of The Polynomial P X X 2 3x 2

Solution Please Help Me 2 If Polynomial P X 2x 3 3x 2 10 Has Exactly One Real Zero R 1 Lt R Lt 1 Which Following Is True A 1 Lt 0 B 0 Lt 1 Or C Other Answer Explain 3 What Is A Portion

If the roots of the equation x 2 p x c = 0 are (2, − 2) and the roots of the equation x 2 b x q = 0 are (− 1, − 2), then the roots of the equation x 2 b x c = 0 are Medium View solutionWithout solving the following quadratic equation, find the value of 'p' for which the given equation has real and equal roots x 2 (p 3)x p = 0 Asked by Topperlearning User 27th Oct, 17, 0224 PMSolution x 2 – 2x – 15 = 0 For x = 5 to be solution of the given quadratic equation it should satisfy the equation So, substituting x = 5 in the given equation, we get LHS = (5) 2 – 2(5) – 15 = 25 – 10 – 15 = 0 = RHS

Divide The Polynomial P X By The Polynomial G X And Find The Quotient And Remainder In Each Of The Following P X X 4 3x 2 4x 5 G X X 2

P X X3 3x2 3x 1 G X X 2 Brainly In

Just enter your equation carefully, like shown in the examples below, and then click the blue arrow to get the result!If the roots of the equation x 2 p x c = 0 are (2, − 2) and the roots of the equation x 2 b x q = 0 are (− 1, − 2), then the roots of the equation x 2 b x c = 0 are Medium View solutionIf P is the solution set of – 3x 4 < 2x – 3, x ∈ N and Q is the solution set of 4x – 5 < 12, x ∈ W, find (i) P ∩ Q (ii) Q – P Answer 33 (i) – 3 x 4 < 2 x – 3 – 3x – 2x < – 3 – 4 => – 5x < – 7 Question 34 A = {x 11x – 5 > 7x 3, x ∈R} and B = {x 18x – 9 ≥ 15 12x, x ∈R}

Systems Of Linear Equations

P X 3x 2 Find The Number Of Zeros Of The Given Polynomial Brainly In

Let P (x) = (x − 3) (x − 5) Q (x) x A B P (3) = 1 0 = 3 A B P (5) = 6 = 5 A B This gives A = − 2, B = 1 6 Thus by division by (x − 5) (x − 3), ans will be − 2 x 1 6 More Items ShareHere, P=y 2 ,Q=xy , R= x(z2y) Hence the general solution is f(x 2 y 2, yzy 2)=0 3Solve(3z4y)p(4x2z)q=2y3x Soln Given (3z4y)p(4x2z)q=2y3x This equation of the form Ppq=R Here, P= (3z4y) ,Q=(4x2z) , R= 2y3x Again use Lagrangian multipliers 2,3,4, 2x3y4z=b Hence the general solution is, F(x 2 y 2 z 2 , 2x3y4z)=0

By Dividing P X 2x 3 3x 2 17x 30 By G X X 3 Show That G X Is A Factor Of P X And Hence Factorize P X Completely

Solution Use The Graph To Solve The Inequality Indicated Write The Answers In Interval Notation P X X 3 4x 2 3x 18 P X Lt 0

Polynomial Functions

5 Solving Polynomial Equations Ppt Download

2

Find Zero Of The Polynomial P X 3x Brainly In

Ncert Solutions For Class 9 Maths Chapter 2 Exercise 2 4 Polynomials

If P X 2x 2 3x 5 3x 5 Then P 1 Is Equal To Math Polynomials Meritnation Com

Let Us Consider Some More Examples Example 7 Divide The Polynomial 3x4 4x 3x 1 By

P X Ax A 0

Remainder Theorem Method Examples

Solved 1 Find The Solution In Z 147z Of 3x 2 13 Chegg Com

Ex 2 2 4 Find The Zero Of The Polynomial In Each Of Ex 2 2

Polynomial Equations

Http Www Math Unl Edu Scohn1 104s07 S3 Pdf

Solving Cubic Equations Solutions Examples Videos

3 Find The Value Ofk If X 1 1 See How To Solve It At Qanda

P X 3x 1 X 1 3 Verify Zeroes Of Polynomial Show Method Also Brainly In

Draw The Graph For The Polynomial P X X 2 3x 2 And Find The Zeroes From The Graph

Using The Remainder Theorem Find The Remainder When P X Is Divided By G X Where P X 2x 3 3x 2 11x 3 G X Left X Dfrac 1 2 Right

2

Identify Polynomials In The Following I F X 4x 3 X 2 3x 7 Ii G X 2x 3 2x 2 X 1 Iii P X 23 X 2 74 X

Kseeb Solutions For Class 9 Maths Chapter 4 Polynomials Ex 4 2 Kseeb Solutions

D Answer The Following2 Given N X X 5 And Brainly Ph

2

Module 1 Polynomial Functions

Ex 2 2 4 Find The Zero Of The Polynomial In Each Of Ex 2 2

Free Solutions For Ncert Cbse Class 9 And Chapter Polynomials And Exercise 02 Doubtnut

Ncert Cbse Maths Class 10 Ex 2 3 Q No 1 Solutions Divide The Polynomial P X By The Polynomial G X And Find The Quotient And Remainder In Each Of The Following Ncert Maths

Tenth Maths Guide For Polynomials Exercise 3 1 3 2 3 3 3 4 Solutions For Class 10 Maths Chapter 3 Maths Glow

Ex 2 2 4 Find The Zero Of The Polynomial In Each Of Ex 2 2

The Product Of Two Zeroes Of Polynomial P X X 3 3x 2 6x 8 Is 2 Find All The Zeroes Of The Polynomial

Suppose A Random Variable X Has A Pmf P X 3 X 1 4 X X 1 Homeworklib

Find All The Zeroes Of P X 2x 4 3x 3 3x 2 6x 2 If You Know That Two Of Its Zeroes Are 2 And 2

Solved Solve The Following Equation For Real Solutions Chegg Com

Find The Value Of P If The Polynomial P X X4 2x3 3x2 Px 3p 7 When Divided By X 1 Leaves The Brainly In

The Solution Of Equation P Q X R Q R X P R P X Q 3x P Q R 0 Is Youtube

Www3 Nd Edu Craicu 1bspring10 Quiz1b Q10 Pdf

Www Ualberta Ca Csproat Homework Math 334 Assignment solutions Assignment 2 solutions Pdf

Loughranmath Weebly Com Uploads 1 1 0 4 cch Rational Zeros Thm 12 01 16 Pdf

Rd Sharma Solutions For Class 10 Chapter 8 Quadratic Equations Exercise 8 6 Avail Pdf

How To Find The Zeros Of The Polynomial P X 3x Brainly In

Solved Example 2 Determine Whether Or Not The Vector Fiel Chegg Com

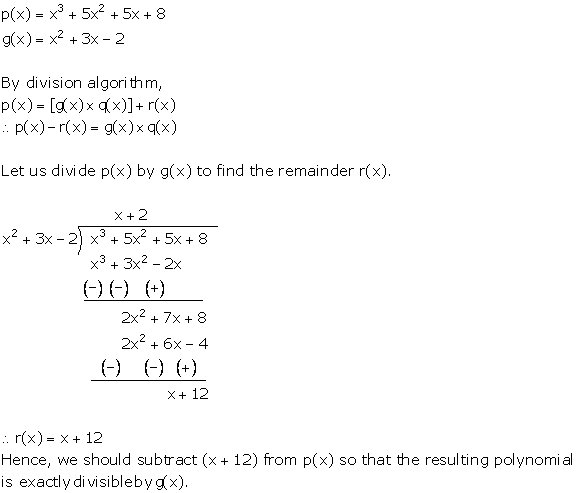
Chapter 8 Polynomials Government Of Karnataka Solutions For Class 10 Mathematics Maharashtra Topperlearning

2

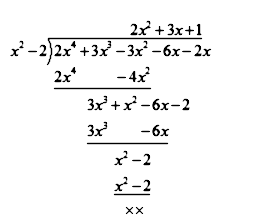
Question Two Zeroes Of The Polynomial P X 2x 4 3x 3 3x 2 6x 2 Text Are Sqrt 2 And Sqrt 2 Find The Remaining Zeroes Of P X If Any Snapsolve

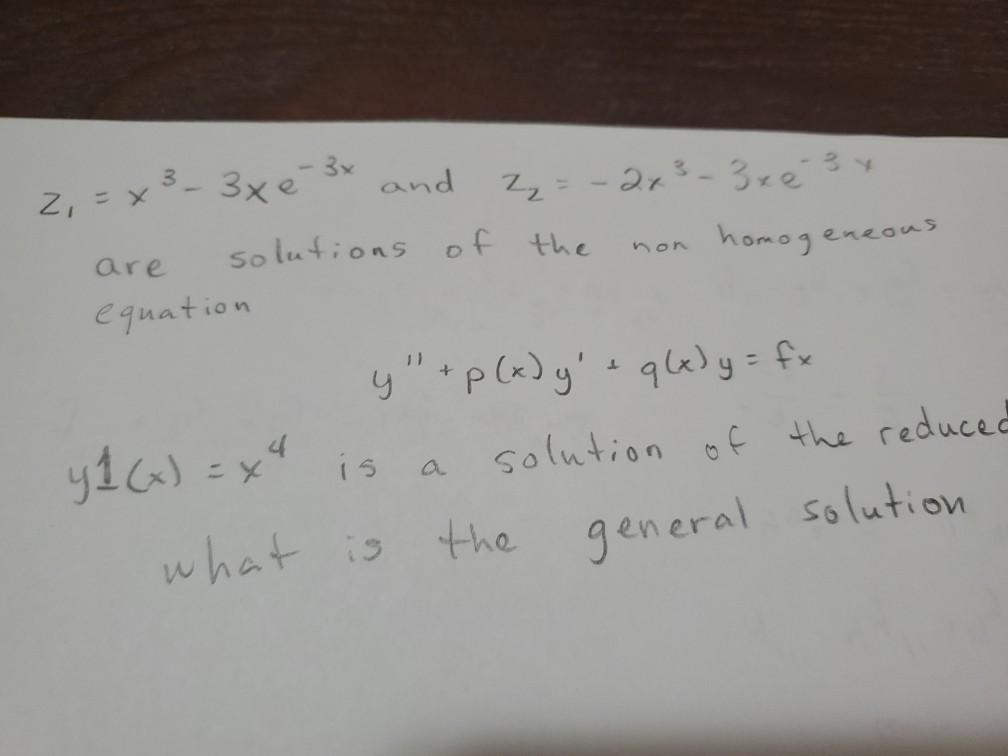
And Non Are Z X3 3xe 3x 2 273 3xe 3x Solutio Chegg Com

For What Value Of P Will The Following System Of Equations Have No Solution 2p 1 X P 1 Y 2p 1 Y 3x 1 0 Sarthaks Econnect Largest Online Education Community

If P X 2x 2 3x 5 Then Find The Value Of P 0 P 1 Whole Devided By P 1 Math Polynomials Meritnation Com

Ex 2 2 4 Find The Zero Of The Polynomial In Each Of Ex 2 2

Pinkmonkey Com Algebra Study Guide 3 2 Monomials Polynomials And Factoring

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials Toppers Bulletin

Unit 1 3 The Remainder Theorem The Burns Home Page

Check Whether G X X 2 3x 1 Is A Factor Of The Polynomial P X 3x 4 5x 2 7x 2 2x 2 By Dividing P X By G X

Rd Sharma Solutions For Class 10 Chapter 8 Quadratic Equations Exercise 8 6 Avail Pdf

Ncert Exemplar Problems Class 9 Maths Polynomials 12 Www Cbsetuts Com Ncert Exemplar Problems Class 9 Maths Polynomia Polynomials Maths Solutions Math

Http Mr Choi Weebly Com Uploads 1 7 0 5 Assignment 2a Solutions Pdf

3 4 Solving Polynomial Equations

Find The Remainder When X3 3x2 3x 1 Is Divided By X 1

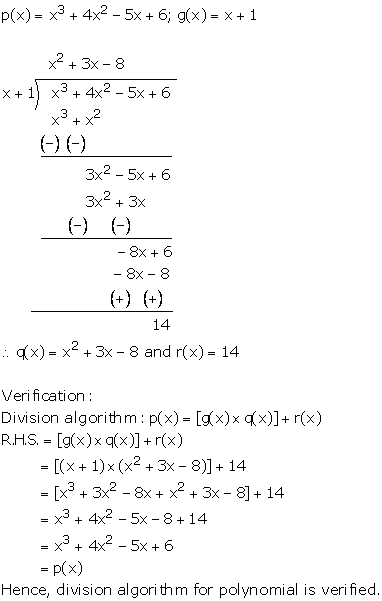
Chapter 8 Polynomials Government Of Karnataka Solutions For Class 10 Mathematics Maharashtra Topperlearning

If P X X 3 3x 2 2x Find P 0 P 1 P 2 What Do You Conclude

Find The Remainder When X 3 3x 2 3x 1 Is Divided By X P Mathematics Shaalaa Com

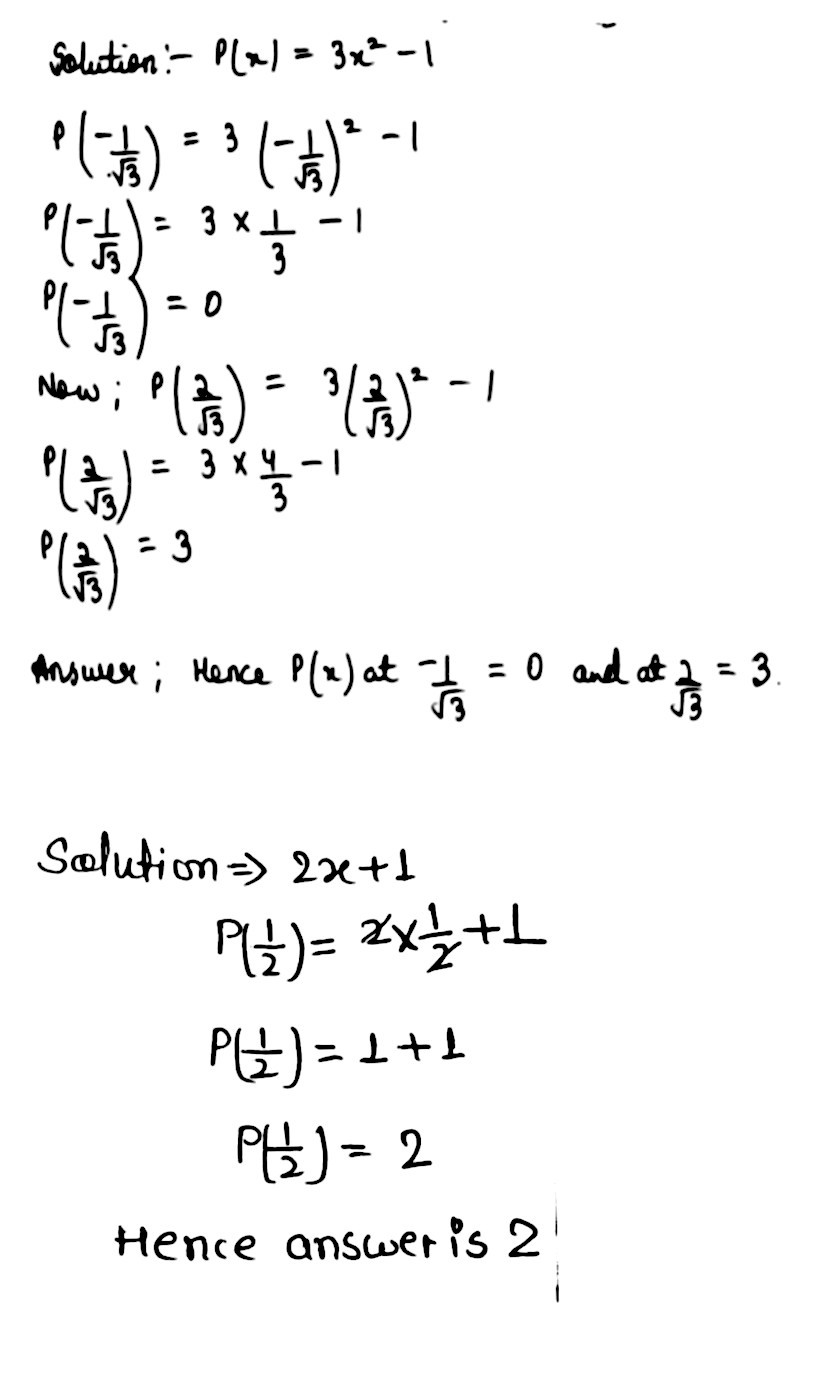
Question Vii P X 3x 2 1 X Frac 1 Sqrt 3 Cdot Frac 2 Sqrt 3 Viii P X 2x 1 X Frac 1 2 Snapsolve

Module 1 Polynomial Functions

Find The Value Of K Such That 3x 2 2kx X K 5 Have The Sum Of Zeros And As Half Of Their Product Edurev Class 10 Question

2xy 3x 2 Dx X 2 2y Dy 0 Wolfram Alpha Clip N Share

Solved C2e6x If The Function 3x 1 And E6xare Solution Chegg Com

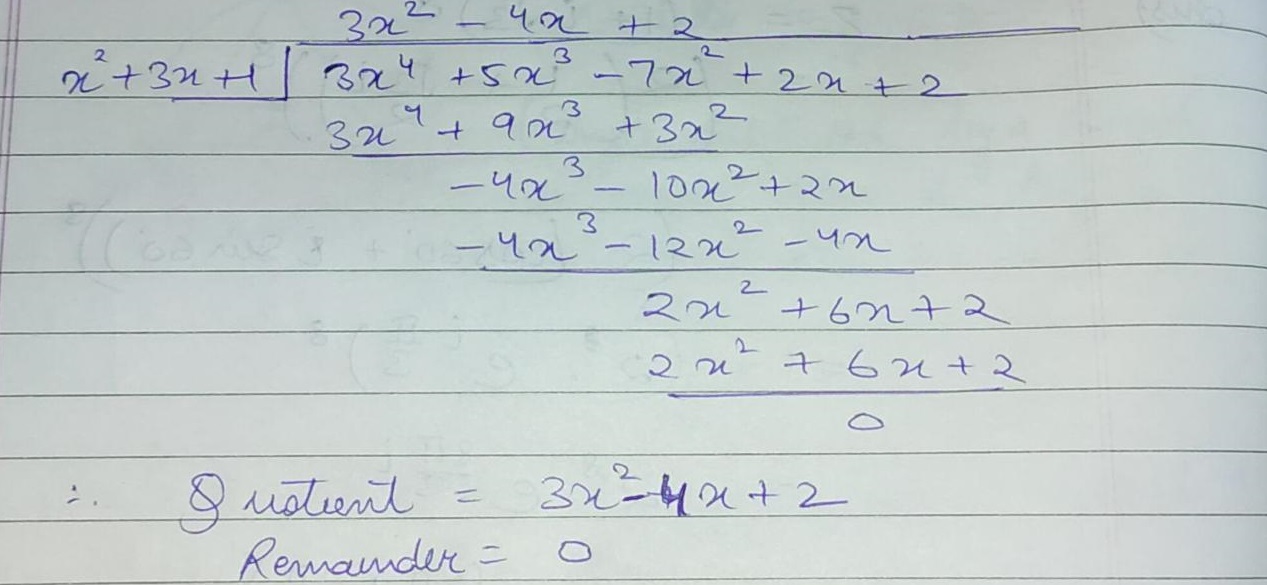
Divide P X 3x 4 5x 3 7x 2 2x 2 By G X X 2 3x 1 And Find The Quotient And Remainder

Module 1 Polynomial Functions

Solution I Need Help Graph The Polynonmial Function P X X 4 X 3 3x 2 5x 2 And Use The Zeros X Intercepts To Find A Factorization Of P X Thanks

If 2 And 2 Are Zeros Of The Polynomial P X Ax 4 2x 3 3x 2 Bx A Find The Value Of A B Math Polynomials Meritnation Com

Find The Zero Of The Polynomial P X 3x 21 Please Give Me A Right Solution And Please Fast Brainly In

Solution Find All Zeros Of The Polynomial Function And Write The Polynomial As A Product Of Its Leading Coefficient And Its Linear Factors P X 3x 5 2x 4 10x 3 6x 2 25x

The Polynomials P X Ax3 4x2 3x 4 And Q X X3 4x A Leave The Same Remainder When Divided By X 3 Find Brainly In

Ncert Solutions For Class 9 Maths Chapter 2 Polynomials In Pdf

Draw The Graph Of P X X 2 3x 4 And Find Zeroes Verify The Zeroes Of The Polynomials

Incoming Term: p(x)=3x solution, p(x)=3x+1 x=-1/3 solution,